
Return Home 気象科学実験教室、一覧表 キッズの気象実験、一覧表 「気象実験クラブ」入会案内。気象実験(#B0)
実験の様子を写真で紹介します。
実験項目および内容は、随時追加、修正、改良しています。 Originated 2008-12/18 Last Updated 2008-12/28, 2009-01/29, 2/08, 2010-01/12
●=EXPMB2 EXPMB0 スピンアップ (ビン、茶がら、水) EXPMB1 静力学のパラドックス (ペットボトル。ビン、台ばかり、水) ●=EXPMB2 流線 (洗面器、ストロー、水、茶がら)(コンピューターシミュレーション) EXPMB3 遠心力と重力の釣り合い (ボール、紐、針金、ボールペン) EXPMB4 台風解析(気象衛星画像) EXPMB5 台風の気流解析(T0423)(高層気象観測データ) EXPMB6 台風のベストトラック(コンピューターシミュレーション)(気象庁やJTWCのベストトラックデータを利用) EXPMB7 トラック作成ツール EXPMB8 エクマンスパイラル (コンピューターシミュレーション) EXPMB9 大気の波動 (コンピューターシミュレーション) |
静力学のパラドックス
|
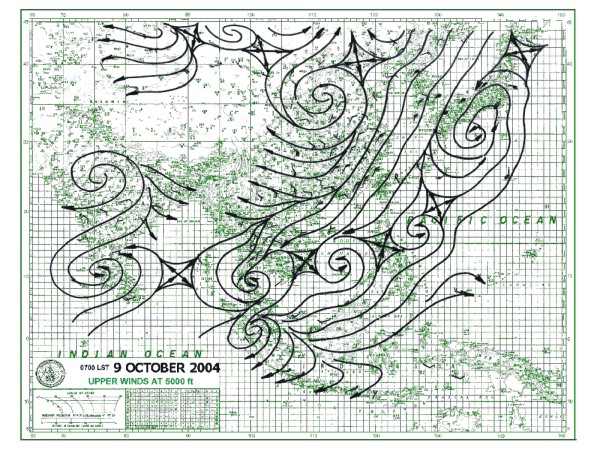 この流線と言う言葉には、兄弟用語として、流脈線、流跡線というものがあります。
それらの用語は、空気の流れにおいて、どのような状態を表現しようとしているのであろうか。
気象や流体力学の教科書、参考書には流線関数とか循環等という用語も出てきて、私には理解
が困難な物です。とにかく、実際に流れを作って、流線とはどんなものかみて、少しでも理解して
おきたいと思っています。こういう実験を行うには、その本質をいかに表現、現出させたらよいか
の問題が付きまといます。実験がうまくできれば、流線というものをある程度理解できたことになる
と思っています。
#B21 実験タイトル=流線
#B22 実験の狙い=流線と言うものをつくり、見る、理解する
●=以下、写真は一部準備中です。
この流線と言う言葉には、兄弟用語として、流脈線、流跡線というものがあります。
それらの用語は、空気の流れにおいて、どのような状態を表現しようとしているのであろうか。
気象や流体力学の教科書、参考書には流線関数とか循環等という用語も出てきて、私には理解
が困難な物です。とにかく、実際に流れを作って、流線とはどんなものかみて、少しでも理解して
おきたいと思っています。こういう実験を行うには、その本質をいかに表現、現出させたらよいか
の問題が付きまといます。実験がうまくできれば、流線というものをある程度理解できたことになる
と思っています。
#B21 実験タイトル=流線
#B22 実験の狙い=流線と言うものをつくり、見る、理解する
●=以下、写真は一部準備中です。

 #B23 実験装置の製作 and/or 準備
・洗面器(あるいは、ペットボトル)、水、茶がら(或いは、醤油、油)を用意します。
・洗面器の水を回転させます。
・茶がらを水面へ静かにふりかけます。
・別途、コンピューターシミュレーションを行い、流線をパソコンのスクリーン上に描いてみます。(下記#B26、参照)
#B24 実験の実行と結果
・水面を流れる茶がらを見て、流線とはどの部分であるのか、を判断します。下の参考図を参照して下さい。
・流脈線、流跡線はどの部分であるか、いかにすれが、目に見えるのか、も同様に考えてみます。(下記#B27、注*)
・参考図:
#B23 実験装置の製作 and/or 準備
・洗面器(あるいは、ペットボトル)、水、茶がら(或いは、醤油、油)を用意します。
・洗面器の水を回転させます。
・茶がらを水面へ静かにふりかけます。
・別途、コンピューターシミュレーションを行い、流線をパソコンのスクリーン上に描いてみます。(下記#B26、参照)
#B24 実験の実行と結果
・水面を流れる茶がらを見て、流線とはどの部分であるのか、を判断します。下の参考図を参照して下さい。
・流脈線、流跡線はどの部分であるか、いかにすれが、目に見えるのか、も同様に考えてみます。(下記#B27、注*)
・参考図:
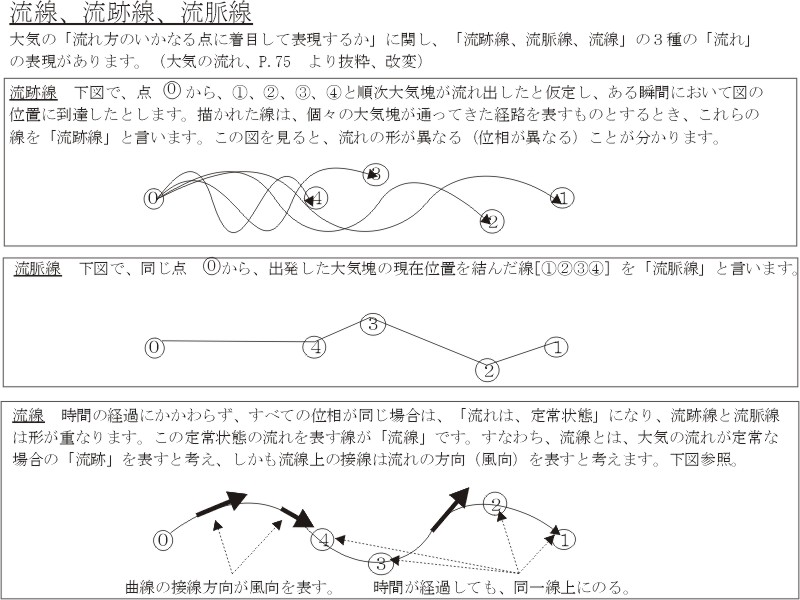 この流線の図をみると、下記#B26の気象力学通論の流線を求める記述が具体的な方法論として理解できます。
#B25 実験を効果的に行うための工夫、注意点等
・上記参考図に示したように、茶がらの落下点は、水面上つねに一定の位置を保つことが肝要です。
・流れの中に障害物を入れてみると、流れは蛇行や渦となり、形がより明瞭になります。
・茶がらは、沈んでしまうこともありますので、代わりに醤油等を使ってみるとよいでしょう。
油を使う場合は、後始末が少々大変かも知れませんが、水面上同一の油、別個の油、数滴の油、
さらには油の列などの形が明瞭に見えますので、おすすめです。
・油を使う場合は、洗面器の代りに、1.5Lの四角いペットボトルを利用します。縦に切り離し水路を作ります。
使い終わったら、簡単に捨てることができます。
この流線の図をみると、下記#B26の気象力学通論の流線を求める記述が具体的な方法論として理解できます。
#B25 実験を効果的に行うための工夫、注意点等
・上記参考図に示したように、茶がらの落下点は、水面上つねに一定の位置を保つことが肝要です。
・流れの中に障害物を入れてみると、流れは蛇行や渦となり、形がより明瞭になります。
・茶がらは、沈んでしまうこともありますので、代わりに醤油等を使ってみるとよいでしょう。
油を使う場合は、後始末が少々大変かも知れませんが、水面上同一の油、別個の油、数滴の油、
さらには油の列などの形が明瞭に見えますので、おすすめです。
・油を使う場合は、洗面器の代りに、1.5Lの四角いペットボトルを利用します。縦に切り離し水路を作ります。
使い終わったら、簡単に捨てることができます。
 ・インクや墨汁も流れのトレーサとして使えますが、後始末が大変です。こぼすと周囲を汚してしまいます。
・流れの様子を、スローシャッターで写真撮影するとよいでしょう。カルマン渦の写真は、一つの例です。
#B26 実験の解説 and/or 関連実験
・流線を通して、流れの性質や流れの表現を考えるきっかけ、糸口になります。
・流体の流れを議論するとき、必ず登場するベルヌーイの定理は、流線に対してのみ成立します。
・地衡風平衡の状態は、流線を議論しています。高層天気図の等高線は、流線に近いと言われています。
・小倉、気象力学通論p.27欄外、によれば、
「速度の2成分がu(x,y,t)、v(x,y,t)で与えられているとすれば、dy/dx=v(x,y,t)/u(x,y,t)という
微分方程式をxについて積分すれば、ある時刻t0 における流線が描ける。」とあります。
私たちは、空気塊の x,y 方向の速度 u,v に関して、数値予報に使われるプリミティブ方程式を知っています。
実験A8、風速の予測 に書きましたが、下記2式です。
①∂u/∂t=-(u∂u/∂x+v∂u/∂y+w∂u/∂z)
+2Ωsinφv-∂p/ρ∂x+Fx
②∂v/∂t=-(u∂v/∂x+v∂v/∂y+w∂v/∂z)
-2Ωsinφu-∂p/ρ∂y+Fy
演算の手順は、dy/dx=v(x,y,t)/u(x,y,t)を変形して、dy=(v(x,y,t)/u(x,y,t))dxと書き直します。
dy=(v(x,y,t)/u(x,y,t))dx、の式を、両辺積分すればy=f(u,v)x+定数、として表現できます。
そして、パソコンのスクリーン上に描くことが出来ます。(ここで、定数=初期値、とします。)
なお、u,vは①②式を積分すれば求められます。手順は、実験A8風速の予測、ですでに確立しています。
ここまでの手順を押さえておけば、あとは今少し数式を整理し、プログラム化し易くします。
あとは、適宜なデータを与えて、パソコンで流線を描くことができそうです。
#B27 【追加実験、考察等】
・風が少しある日、(銭湯などの)煙突の煙の形を観察してみよう。
・煙突がなければ、自宅の台所で、やかんの口から出てくる湯気の形を観察して見よう。
・これらの形は、「流線、流脈線、流跡線」のどれに相当するのだろうか。
・或いは、一定高度で風に流される風船、ラジオゾンデ、パイロットバルーン等も空気の流線を
示すトレーサーになると考えられます。
・さらには、水面にできるカルマン渦や、水中で見る水の熱対流の様子も、そこに流線の
形成・存在を考えることができます。
(注記*:流線に関しては、拙著、「大気の流れ」P.75 及びP.117 に説明しています。)
先頭へ戻る 気象科学実験教室、一覧表 キッズの気象実験、一覧表
・インクや墨汁も流れのトレーサとして使えますが、後始末が大変です。こぼすと周囲を汚してしまいます。
・流れの様子を、スローシャッターで写真撮影するとよいでしょう。カルマン渦の写真は、一つの例です。
#B26 実験の解説 and/or 関連実験
・流線を通して、流れの性質や流れの表現を考えるきっかけ、糸口になります。
・流体の流れを議論するとき、必ず登場するベルヌーイの定理は、流線に対してのみ成立します。
・地衡風平衡の状態は、流線を議論しています。高層天気図の等高線は、流線に近いと言われています。
・小倉、気象力学通論p.27欄外、によれば、
「速度の2成分がu(x,y,t)、v(x,y,t)で与えられているとすれば、dy/dx=v(x,y,t)/u(x,y,t)という
微分方程式をxについて積分すれば、ある時刻t0 における流線が描ける。」とあります。
私たちは、空気塊の x,y 方向の速度 u,v に関して、数値予報に使われるプリミティブ方程式を知っています。
実験A8、風速の予測 に書きましたが、下記2式です。
①∂u/∂t=-(u∂u/∂x+v∂u/∂y+w∂u/∂z)
+2Ωsinφv-∂p/ρ∂x+Fx
②∂v/∂t=-(u∂v/∂x+v∂v/∂y+w∂v/∂z)
-2Ωsinφu-∂p/ρ∂y+Fy
演算の手順は、dy/dx=v(x,y,t)/u(x,y,t)を変形して、dy=(v(x,y,t)/u(x,y,t))dxと書き直します。
dy=(v(x,y,t)/u(x,y,t))dx、の式を、両辺積分すればy=f(u,v)x+定数、として表現できます。
そして、パソコンのスクリーン上に描くことが出来ます。(ここで、定数=初期値、とします。)
なお、u,vは①②式を積分すれば求められます。手順は、実験A8風速の予測、ですでに確立しています。
ここまでの手順を押さえておけば、あとは今少し数式を整理し、プログラム化し易くします。
あとは、適宜なデータを与えて、パソコンで流線を描くことができそうです。
#B27 【追加実験、考察等】
・風が少しある日、(銭湯などの)煙突の煙の形を観察してみよう。
・煙突がなければ、自宅の台所で、やかんの口から出てくる湯気の形を観察して見よう。
・これらの形は、「流線、流脈線、流跡線」のどれに相当するのだろうか。
・或いは、一定高度で風に流される風船、ラジオゾンデ、パイロットバルーン等も空気の流線を
示すトレーサーになると考えられます。
・さらには、水面にできるカルマン渦や、水中で見る水の熱対流の様子も、そこに流線の
形成・存在を考えることができます。
(注記*:流線に関しては、拙著、「大気の流れ」P.75 及びP.117 に説明しています。)
先頭へ戻る 気象科学実験教室、一覧表 キッズの気象実験、一覧表
ボール2個を紐で結び、吊り下げる
| 鉛直面内の回転
| 水平面内の回転
|
1.T0511(MAWAR:バラ[マレーシア]) (2005年08月20日発生、09月05日事後解析した。) 3.T0513(TALIM:鋭い刃先[フィリピン]) (2005年08月27日発生~09月02日解析終了。) 4.T0514(NABI:ちょう(蝶) [韓国]) (2005年08月29日発生~09月08日解析終了。) 5.T0515(KHANUN:果物の名前、バラミツ [タイ] ) (2005年09月07日発生~09月15日解析終了。) 6.T0516(VICENTE:女性名称 [米国] ) (2005年09月16日発生~09月19日解析終了。) 7.T0517(SAOLA:動物の名前 [ベトナム] ) (2005年09月21日発生~09月27日解析終了。) 9.T0519(Longwang :龍の王 [中国] ) (2005年09月26日発生~10月03日解析終了。) |
3.T0513(TALIM:鋭い刃先[フィリピン]) (2005年08月27日発生~09月02日解析終了。)ドボラック法による台風解析の試行 Return to Top page 台風解析、解析手順・前提 CI数 Originated: 2005-08/29, Last Updated: 2005-09/02 |
1.台風になりそうな前からTDの雲画像を眺めておく(アーカイブしておく)。 (私は、IR画像をみて、風速17.2m/s 以上になったことを確認する手段を 持たないので、気象庁の台風発表を絶えず注意しておき、台風発生時点の画像や強度の 情報をアーカイブしておく。及び、USのNational Hurricane Center のINVEST 情報も参考になるので眺めておく。) 2.台風発生時点のCI数は、通常CI=2.0或いはこの数値の前後である。 気象庁発表の最大風速と中心気圧から、CI数をCI数の「換算表」から逆に求めることとする。 このとき、本HPでは、最大風速を基準として、CI数を定めることにする。 (気圧よりも、風速の方が信頼性が高いと思われるので。) 3.台風として発表された時点で、その1日前の状態をPT雲パターンから決定し、 そのPT数を「一番最初のMET数」とする(なお、1.0日前の時点を、MET=1.0 とするのが原則である)。 即ち、台風発生とされた1.0日前を(さかのぼって)解析スタート時点とする。 このHPにおいて、画像のアーカイブが無い場合は、半日前の画像からスタートする こともあり、この場合の発達の程度の数値は、按分する。 4.MET数は、標準的な発達では、1日につき、1.0増加するが、増減幅は±1.5 である。 (特に、外周直径の増減、スパイラルの有無(及び長さ、巻き数、スパイタル中のCb雲の存在)、 中心付近の雲頂高度の増減、濃密な雲域の拡大縮小、が発達衰弱の判断のポイントとなる。 但し、以上は大分「主観的」である。ほかにも判断のポイントがあるかも知れない。 詳細は、下記テキスト等を参照。 (なおNHCでは、客観的判断にすべくODTと言う手法を開発している。後述) 雲が無定形に広がっていて、次第に、正回転を始めたときは、TDの卵の時期である。 濃密な雲域が薄くなってきたときは、衰弱傾向にある。 NHCのMulti画像も大変参考になる。) 5.台風の中心位置は、IRやVISでは、雲の回転状況やスパイラルから 曲率中心を目算で求める。眼が形成されていれば、眼を中心と考える。 6.眼が形成された場合、DT数は少なくともDT=4.0 でなければならない。 そこでMET数も、MET=4.0以上であることを確認する。 自分の推定値が、MET=4.0以下の場合は、雲画像の見方を誤っていた可能性がある。 7.台風が、陸地に上陸した場合は、ドボラック法の採用は困難となるので、 上陸以降の強度推定は、通常(筆者は)この時点で終了する。台風が陸地から海洋上に 抜け出した場合は、地上観測を参考にして、強度の解析を再開することもある。 |
・毎時の画像を連続的に観察し、「発達傾向、衰弱傾向」の「心象」を得ておくことが 大事なようです。発達と衰弱の判断を誤ると、気象庁発表の値と大きくズレてしまう ことがあります。 台風画像に慣れるためには、いろんな台風のライフサイクルの画像をよく見ることである。 すべてを網羅したものではないが、この数週間の間に発生した台風4種の画像をまとめました。 ・台風が、陸上に上陸 landfall したときの強度推定は、地上観測に任せるべきである。 ドボラック法は、地上観測が不可能な海洋上において、意味があります。 ・雲画像の面積が拡大しても、必ずしも、強度増加と判断できないことも あるようなので、注意(熟練?)を要す。 ・雲域が衰弱傾向にあるときは、注意を要する。このときは、T数の減少よりも タイムラグを設けてCI数を減少させる必要がある(経験的、統計的観点より)。 ・台風発生とする風速 17.2m/s はいかにして特定するのだろうか? QuickScatか? ・US-NavyのWeb siteでは、詳細は分かりませんが、「INVEST」の表示で ハリケーンや台風の「候補」を常にモニターしているようです。 |
■ 「台風の眼」が形成される時点の遅速に関しての考察 ほぼ同時的に誕生したT0517 Saola とT0518 Damrey のライフサイクルを比較してみるとき、 T0517の眼は、誕生してまもなく明瞭になったが、T0518 の方は、「3日遅れ」で眼が出来た。 先ず、共通して言えることは、「眼の形成」のためには、渦巻きの回転が必要であること。 逆に言うならば、赤道付近の積乱雲群は、対流現象は盛んで、雲が無定形に広がるが、 全体としては、ほとんど回転せず(組織化されず、と換言してもよい)「眼」が形成されない。 T0518の眼の形成が「3日遅れ」となった原因は、それぞれの進行した経路および海水面の 温度の違いによるものと考えます。とりわけ、緯度の相違(コリオリ力の大小)が渦巻きの形成、 したがって、眼の形成時点の遅速につながったものと推定します。 ■ 北上スピードと台風の発達の程度 この状況が示唆するところのものは(まだ断定的にはいえないが)、急速に北上する 台風と、北上せず西進する台風とでは、発達の仕方(即ち雲画像での見かけ上の形の変化)が 異なることである。 また急速に北上しても眼が形成されない台風もある→T0512(T0511と一時的に併進・北上した)。 これは、渦全体の規模・供給されるエネルギー総量の大小によるのではないかと推定するが、 推定の域を出ない。 ■ 衰弱期の台風の眼の位置と雲域の関係 台風は衰弱期に入ると、雲は上層の偏西風に流され、渦の中心軸からはなれ、先行して北東進 する場合が多い。雲域の中心と地上の最低気圧を示す中心とは数百km以上はなれることもある。 この時期の台風の構造に関しては、2005年10月02日、日本気象予報士会神奈川支部主催の 「第3回ウィンドプロファイラー勉強会」で話する予定です。 ■ 台風を動かす力と運動 低緯度で発生した台風が何故、北上するか、西進するかの議論には理解しがたいものが多いが、 断片的理解ではあるが次のことは言えるであろう: 1.低緯度にあっては、貿易風が西向きの力を与える。 2.低緯度から中緯度にかけては太平洋高気圧から吹きだす縁辺流が、西向き、北向き、東向き のいずれかの方向の力を与える。 3.転向点付近からは、偏西風が東~北東方向の力を与える。 4.台風自体は一つのおおきな対流現象であると考えられるが、この対流は、周りの大気を吸い込み、 上層で発散する。このとき、この対流現象は、自分の重心を駆動する力を生じることはないもの と考えられる。 5.台風を巨大質量を有する物体と考え、その重心は上記の力を得て、「慣性」を持って運動する、 と考える。このとき、台風は、一旦動き出したら、容易にとまらない。進行右側に重心がずれて いく、と考えられる。 ■ 擬似射流現象 台風のライフサイクルの発達期、最盛期においては(発達初期や衰弱期には見受けられないが)、 最上層における気流の発散状況を見ると、広がりの先端にやや細い弧状かつ線状の雲がしばしば 見受けられる。→T0919-092909jstの眼から東側500Km付近の線状のやや顕著な雲の帯に注目 これは、水理学で言うところの「射流」に引き続く「跳水」現象に類似しているように考えられる。 この線状の部分は(先端付近の雲は)上昇しているものと考える。理由は、輝度温度が低く、すなわち、 上昇し温度低下となった。そして白く写っていると考えます。そして、やがて下降し、終局的には消えて 見えなくなる、と考えます。 一つの研究課題となるかも知れない。 |
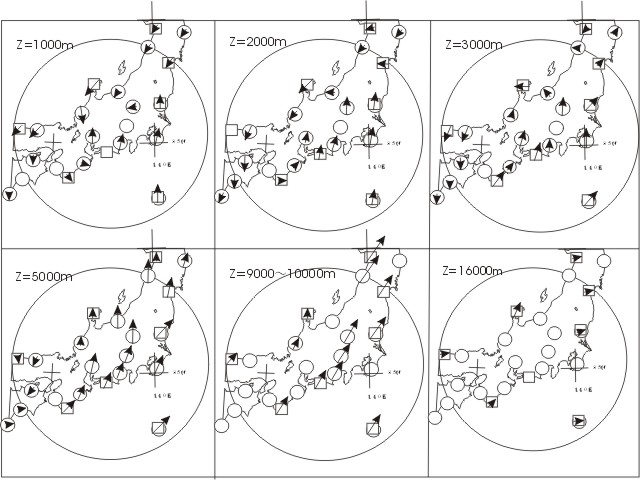 #B53 実験装置の製作 and/or 準備
・高層気象観測データ(T0423)をインターネットから入手します。
・日本地図の準備が必要です。
#B54 実験の実行と結果
・得たデータを日本地図の上にプロットします。
・高層気象観測データ(T0423)を使って、高度別に風向・風速をプロットします。
#B55 実験を効果的に行うための工夫、注意点等
・日本地図を予め作成しておきます。
#B56 実験の解説 and/or 関連実験
・台風の風は、外周から中心に向かう強い気圧傾度力+コリオリ力+遠心力により形成される傾度風であるが、中心近傍では、
コリオリ力より遠心力が強くいので、旋衡風となる。地表面での台風の風は、山岳等の凹凸が「マサツ力」として
作用するので、風速が弱められたり、渦や反流となる。或いは、地形効果により、風速が強化される場合もある。
山岳等で分流した気流による合流、衝突等により、渦、シアーの形成等もある。
・風の観測値(上図)を見ると、上層は自由大気で、風向はほぼそろっている。高度1万メートル近辺で最大風速となっていて、
高度を下げるにつれ、回転している様子がハッキリしてくる。
地表面の山間部での風速は、マサツにより大幅に速度が減少させられる。
渦、反流もあると考えられる。又、山越え気流によるフェーン現象もおき易い。海岸部においては、
海から上がったところでは、風速が強い傾向がある。
・台風の気流は、高度によって流れる方向が異なります。
・特に地表面と高層の場合とでは、特徴的な流れが見受けられます。下記気流解析参照。
・台風の地表面での気流解析(T0423)
■ 台風23号(2004年10月)のときの中部地方、関東地方の地表面の風向をアメダスデータを
元にして流線を描きこみました。外周の円は、レーウィンゾンデの観測値を元にして、上層の
大気の流れを推定して描いたものです。外周と内部の風速差、気流の変化方向に注目します。
#B53 実験装置の製作 and/or 準備
・高層気象観測データ(T0423)をインターネットから入手します。
・日本地図の準備が必要です。
#B54 実験の実行と結果
・得たデータを日本地図の上にプロットします。
・高層気象観測データ(T0423)を使って、高度別に風向・風速をプロットします。
#B55 実験を効果的に行うための工夫、注意点等
・日本地図を予め作成しておきます。
#B56 実験の解説 and/or 関連実験
・台風の風は、外周から中心に向かう強い気圧傾度力+コリオリ力+遠心力により形成される傾度風であるが、中心近傍では、
コリオリ力より遠心力が強くいので、旋衡風となる。地表面での台風の風は、山岳等の凹凸が「マサツ力」として
作用するので、風速が弱められたり、渦や反流となる。或いは、地形効果により、風速が強化される場合もある。
山岳等で分流した気流による合流、衝突等により、渦、シアーの形成等もある。
・風の観測値(上図)を見ると、上層は自由大気で、風向はほぼそろっている。高度1万メートル近辺で最大風速となっていて、
高度を下げるにつれ、回転している様子がハッキリしてくる。
地表面の山間部での風速は、マサツにより大幅に速度が減少させられる。
渦、反流もあると考えられる。又、山越え気流によるフェーン現象もおき易い。海岸部においては、
海から上がったところでは、風速が強い傾向がある。
・台風の気流は、高度によって流れる方向が異なります。
・特に地表面と高層の場合とでは、特徴的な流れが見受けられます。下記気流解析参照。
・台風の地表面での気流解析(T0423)
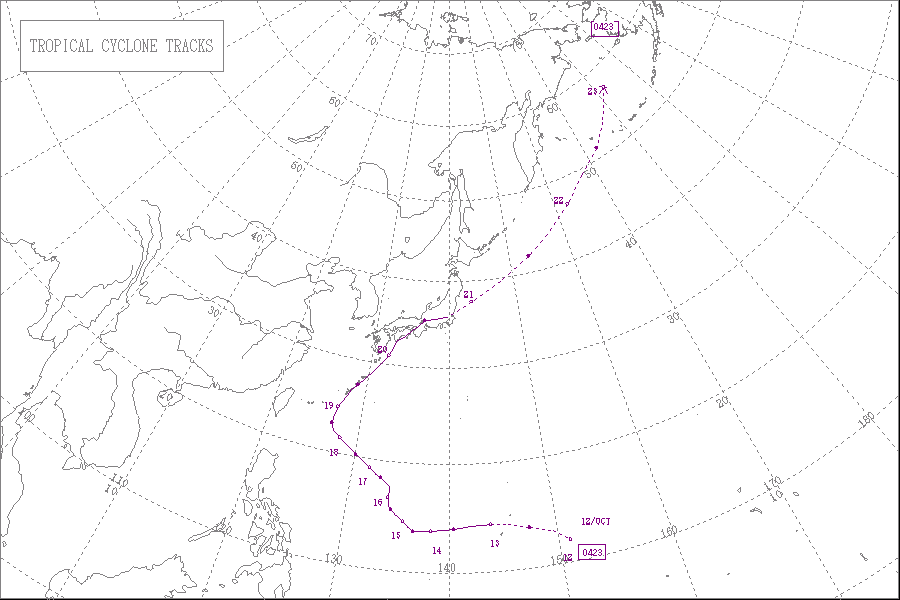
■ 台風23号(2004年10月)のときの中部地方、関東地方の地表面の風向をアメダスデータを
元にして流線を描きこみました。外周の円は、レーウィンゾンデの観測値を元にして、上層の
大気の流れを推定して描いたものです。外周と内部の風速差、気流の変化方向に注目します。
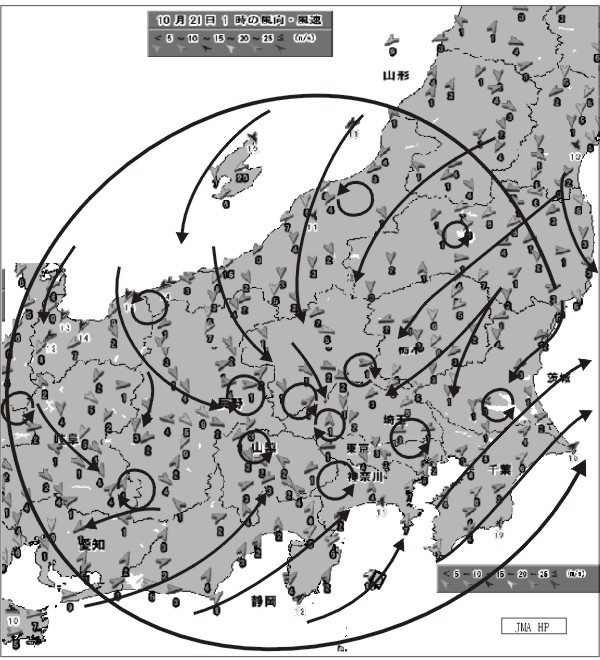 #B57 【追加実験、考察等】
・気象庁作成のベストトラック(T0423):
#B57 【追加実験、考察等】
・気象庁作成のベストトラック(T0423):
 先頭へ戻る 気象科学実験教室、一覧表 キッズの気象実験、一覧表
先頭へ戻る 気象科学実験教室、一覧表 キッズの気象実験、一覧表
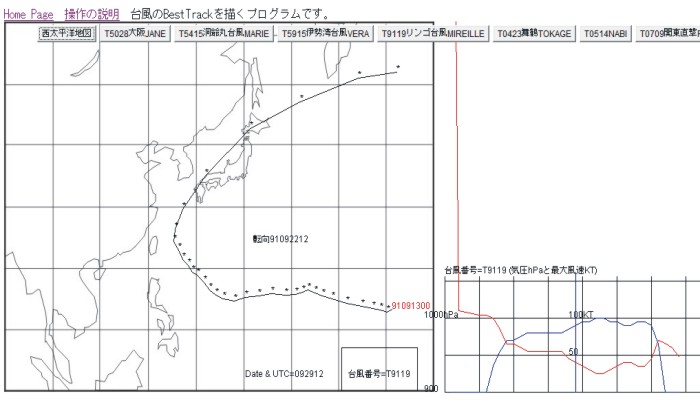 #B63 実験装置の製作 and/or 準備
・パソコンを準備し、インターネットに接続します。
・顕著な台風のベストトラックを描く
●= ===プログラム修正中です。余分な線や数値が表示されることがあります。===
#B64 実験の実行と結果
・白地図或いは天気図上に、ベストトラックを描くことが出来ます
・操作:
★最初は、白地図が表示されます。
★任意の台風をボタン選択します。天気図が表示されます。
(前回描いたトラックが表示されることがありますが、右クリックすると初期状態になります。)
★マウスクリックするたびにトラックが天気図上に描かれていきます。同時に気圧、最大風速のグラフも描かれます。
★天気図上でトラックを描いている時、右クリックする(1回或いは2回押す)と、白地図に戻ります。
戻った白地図上で、マウスクリックすると、同じ台風のトラックを描くことができます。
このとき、台風のボタンを押すとトラックは残ったまま、天気図が描かれ、さらにクリックを続行できます。
★操作が分からなくなったら、マウスの右クリックを(1回または2回)押してみて下さい。
#B65 実験を効果的に行うための工夫、注意点等
・台風の進路を決める要素は何かを考えながら、クリックしてみましょう。
・気圧配置や等高度線との関連に注目しましょう。
・この実験のプログラムは、マウスクリックしながら現象(台風)の進行を(止めながら)PC画面上で見ることができます。
そこで、ある地点まで進行して来た現象(台風)が、今後いかなる要因によって、いかなる進路をとるかの話がし易くなります。
・さらには、台風が本土に接近してきたとき、本土の手前で止めて、風や雨の観点から、防災の話につなげることができます。
#B66 実験の解説 and/or 関連実験
・台風は防災上その進路が大変重要な情報になります。各種の気象資料と付き合わせて検討・研究します。
・関連する解析→台風T0514(NABI)に関しては、ドボラック法による解析を試行しています。ご参照ください。
#B67 【追加実験、考察等】
・台紙となる地図には様々な物があります。
・任意の投影法で作成された地図上に、台風、温帯低気圧さらには物体の運動の軌跡をPC上に描くためには、工夫が必要です。
このため、実験B7でそのひとつの方法を紹介します。
・台風が北上する理論に関しては、私は、実験65、平板斜面上のコマの運動 で示すように考えています。
先頭へ戻る 気象科学実験教室、一覧表 キッズの気象実験、一覧表
#B63 実験装置の製作 and/or 準備
・パソコンを準備し、インターネットに接続します。
・顕著な台風のベストトラックを描く
●= ===プログラム修正中です。余分な線や数値が表示されることがあります。===
#B64 実験の実行と結果
・白地図或いは天気図上に、ベストトラックを描くことが出来ます
・操作:
★最初は、白地図が表示されます。
★任意の台風をボタン選択します。天気図が表示されます。
(前回描いたトラックが表示されることがありますが、右クリックすると初期状態になります。)
★マウスクリックするたびにトラックが天気図上に描かれていきます。同時に気圧、最大風速のグラフも描かれます。
★天気図上でトラックを描いている時、右クリックする(1回或いは2回押す)と、白地図に戻ります。
戻った白地図上で、マウスクリックすると、同じ台風のトラックを描くことができます。
このとき、台風のボタンを押すとトラックは残ったまま、天気図が描かれ、さらにクリックを続行できます。
★操作が分からなくなったら、マウスの右クリックを(1回または2回)押してみて下さい。
#B65 実験を効果的に行うための工夫、注意点等
・台風の進路を決める要素は何かを考えながら、クリックしてみましょう。
・気圧配置や等高度線との関連に注目しましょう。
・この実験のプログラムは、マウスクリックしながら現象(台風)の進行を(止めながら)PC画面上で見ることができます。
そこで、ある地点まで進行して来た現象(台風)が、今後いかなる要因によって、いかなる進路をとるかの話がし易くなります。
・さらには、台風が本土に接近してきたとき、本土の手前で止めて、風や雨の観点から、防災の話につなげることができます。
#B66 実験の解説 and/or 関連実験
・台風は防災上その進路が大変重要な情報になります。各種の気象資料と付き合わせて検討・研究します。
・関連する解析→台風T0514(NABI)に関しては、ドボラック法による解析を試行しています。ご参照ください。
#B67 【追加実験、考察等】
・台紙となる地図には様々な物があります。
・任意の投影法で作成された地図上に、台風、温帯低気圧さらには物体の運動の軌跡をPC上に描くためには、工夫が必要です。
このため、実験B7でそのひとつの方法を紹介します。
・台風が北上する理論に関しては、私は、実験65、平板斜面上のコマの運動 で示すように考えています。
先頭へ戻る 気象科学実験教室、一覧表 キッズの気象実験、一覧表
①データ変換プログラム
| ②ベストトラック表示プログラム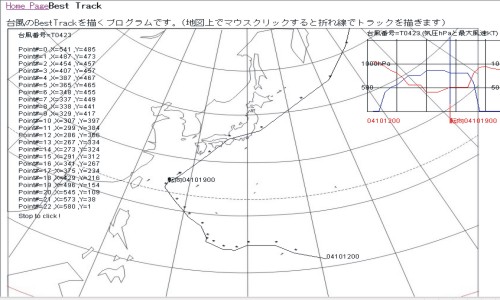
|
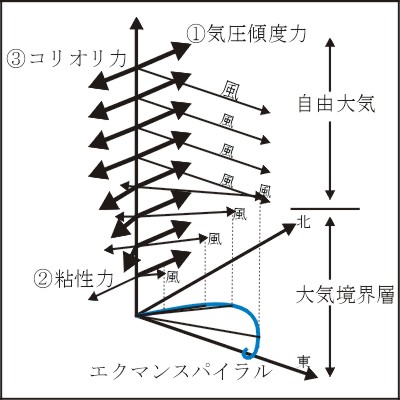 #B81 実験タイトル=エクマンスパイラル
#B82 実験の狙い=エクマンスパイラルを描き、同時に境界層の存在を考え、確かめる
エクマンスパイラル
#B81 実験タイトル=エクマンスパイラル
#B82 実験の狙い=エクマンスパイラルを描き、同時に境界層の存在を考え、確かめる
エクマンスパイラル
 #B83 実験装置の製作 and/or 準備
・スピンアップ、スピンダウンの実験で、渦の立ち上がりを確認する。
・その時、容器底面において、容器の中心へ向かう流れが必須であることを再確認する。
#B84 実験の実行と結果
・パソコンでシミュレーションし、論理式が提供する空気の流れ方を描き、
実空間へ考え方を敷衍する。
・エクマンスパイラルの開始点とスパイラルの線上を結ぶ線が、風向を表していることを
確認します。
#B85 実験を効果的に行うための工夫、注意点等
・エクマンスパイラルの意味するところと、関連分野をよく理解・納得しておこう。
#B86 実験の解説 and/or 関連実験
・スピンアップ、スピンダウン、剛体回転の各実験を再度行い、境界層の存在と
流体の流れの方向を確認しよう。
#B87 【追加実験、考察等】
・
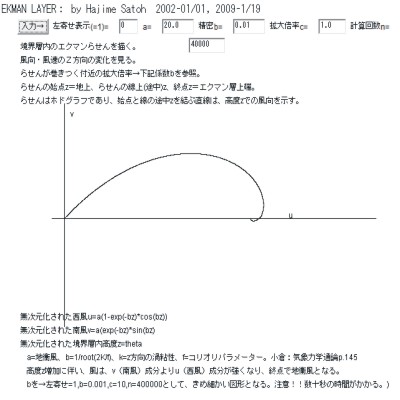
境界層内のエクマンらせんを描く。
風向・風速のZ方向の変化を見る。
らせんが巻きつく付近の拡大倍率→下記係数bを参照。
らせんの始点z=地上、らせんの線上(途中)z、終点z=エクマン層上端。
らせんはホドグラフであり、始点と線の途中zを結ぶ直線は、高度zでの風向を示す。
無次元化された西風u=a(1-exp(-bz)*cos(bz))
無次元化された南風v=a(exp(-bz)*sin(bz)
無次元化された境界層内高度z=theta
a=地衡風、b=1/root(2K/f)、k=z方向の渦粘性、f=コリオリパラメーター。小倉:気象力学通論p.145、トリトン:流体力学p.285
高度z増加に伴い、風は、v(南風)成分よりu(西風)成分が強くなり、終点で地衡風となる。
bを→左寄せ=1,b=0.001,c=10,n=400000として、きめ細かい図形となる。注意!!数十秒の時間がかかる。
先頭へ戻る 気象科学実験教室、一覧表 キッズの気象実験、一覧表
#B83 実験装置の製作 and/or 準備
・スピンアップ、スピンダウンの実験で、渦の立ち上がりを確認する。
・その時、容器底面において、容器の中心へ向かう流れが必須であることを再確認する。
#B84 実験の実行と結果
・パソコンでシミュレーションし、論理式が提供する空気の流れ方を描き、
実空間へ考え方を敷衍する。
・エクマンスパイラルの開始点とスパイラルの線上を結ぶ線が、風向を表していることを
確認します。
#B85 実験を効果的に行うための工夫、注意点等
・エクマンスパイラルの意味するところと、関連分野をよく理解・納得しておこう。
#B86 実験の解説 and/or 関連実験
・スピンアップ、スピンダウン、剛体回転の各実験を再度行い、境界層の存在と
流体の流れの方向を確認しよう。
#B87 【追加実験、考察等】
・
境界層内のエクマンらせんを描く。
風向・風速のZ方向の変化を見る。
らせんが巻きつく付近の拡大倍率→下記係数bを参照。
らせんの始点z=地上、らせんの線上(途中)z、終点z=エクマン層上端。
らせんはホドグラフであり、始点と線の途中zを結ぶ直線は、高度zでの風向を示す。
無次元化された西風u=a(1-exp(-bz)*cos(bz))
無次元化された南風v=a(exp(-bz)*sin(bz)
無次元化された境界層内高度z=theta
a=地衡風、b=1/root(2K/f)、k=z方向の渦粘性、f=コリオリパラメーター。小倉:気象力学通論p.145、トリトン:流体力学p.285
高度z増加に伴い、風は、v(南風)成分よりu(西風)成分が強くなり、終点で地衡風となる。
bを→左寄せ=1,b=0.001,c=10,n=400000として、きめ細かい図形となる。注意!!数十秒の時間がかかる。
先頭へ戻る 気象科学実験教室、一覧表 キッズの気象実験、一覧表
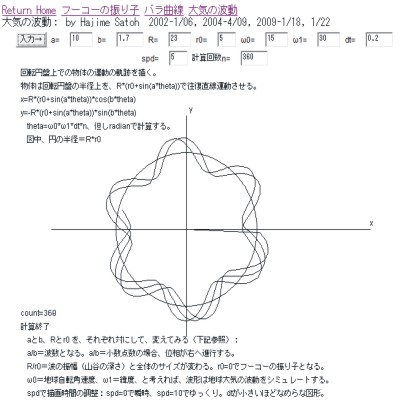 #B93 実験装置の製作 and/or 準備
・このシミュレーションは、フーコーの振り子のプログラムを原典として、
半径方向の往復直線運動を追加したものです。
・下記#B97で、(ペットボトル、水)、(食パン、蜂蜜)、(鎖、回転円盤)、(アルミ粉、回転円盤)を使って行う実験を紹介します。
#B94 実験の実行と結果
・波数、回転角速度、緯度などを変化させると、図形の形が対応して変化します。
・位相がずれていく様子を見ることができます。
#B95 実験を効果的に行うための工夫、注意点等
・実際の空間そのもののサイズと時間をパソコン上で実現することはできない。
・時間やサイズは縮小され、表示される。パソコン上では、見やすさのため適宜値を変えてみます。
・しかし、運動の基礎となる論理は、自然界の物体の運動をシミュレートしている
と考えられます。
#B96 実験の解説 and/or 関連実験
・回転円盤上で、半径方向に往復直線運動する物体の軌跡を描きました。
・熱力学的効果は組み込んでいない。しかし、空気の流れが、ヒマラヤやロッキーの
山脈により変形され、蛇行が励起されたものとして考えてもよさそうです。
・位相の「ずれ」は、大気波動が西進する話について、現実味を帯びさせてくれます。
#B97 【追加実験、考察等】
・この実験は、フーコーの実験の延長線上にあります。
・ペットボトルに水を入れ、さかさまにすると、水がこぼれます。
①このとき、自分が地面に立ってじっとしたままでいると、水は1点に落下します。
②自分が一回転すると、地面には円が描かれます。
③自分がじっとしたままで、ボトルを単振動させると、地面には直線が描かれます。
④単振動させながら、自分が一回転すると、地面には波動が描かれます。
・四角い食パンを回しつつ、上から蜂蜜をたらしてみましょう。
上記①~④において、自分が食パン、水が蜂蜜になったとみなせば、同じ原理の実験になります。
(この実験に引き続き、食パン=>カロリーやエネルギー、蜂蜜=>流体の粘性、の話や実験に移行します。)
・回転円盤上で鎖を垂下させ、単振動させつつ下げていくと、波動が描かれます。(紐やネックレスでもOKです。)
この実験は、新聞紙を広げ、数人が新聞紙回転担当、一人が鎖の垂下・単振動担当、一人が、全体号令担当に
なって、協働して行うと、リチャードソンの数値予報計算の人海戦術の様子を再現するようなもの、となります。
位相がずれていく様子、及びずれに寄与する要因も体感できます。
・回転流体の中の対流の実験装置です:(詳細は → こちら を見てください。)
円盤と3重の水槽で、蛇行する波を作りました。波動の模様は、アルミの粉末で可視化しています。
円盤の駆動には模型用のモーターを組み立てて使っています。この実験は、Dishpan Experiment と
して有名です。同様実験は、数理解析研究所講究録800巻1992年119-128「傾斜対流実験で得られた
カオスへの遷移」等にも見受けられます。
私の実験装置で得られた蛇行の模様です。回転数、温度差、深さ、アルミ粉の散布程度等によって
波数が変わります。又、蛇行現象にならなかったり、なかなか蛇行に移行しないこともあります。
#B93 実験装置の製作 and/or 準備
・このシミュレーションは、フーコーの振り子のプログラムを原典として、
半径方向の往復直線運動を追加したものです。
・下記#B97で、(ペットボトル、水)、(食パン、蜂蜜)、(鎖、回転円盤)、(アルミ粉、回転円盤)を使って行う実験を紹介します。
#B94 実験の実行と結果
・波数、回転角速度、緯度などを変化させると、図形の形が対応して変化します。
・位相がずれていく様子を見ることができます。
#B95 実験を効果的に行うための工夫、注意点等
・実際の空間そのもののサイズと時間をパソコン上で実現することはできない。
・時間やサイズは縮小され、表示される。パソコン上では、見やすさのため適宜値を変えてみます。
・しかし、運動の基礎となる論理は、自然界の物体の運動をシミュレートしている
と考えられます。
#B96 実験の解説 and/or 関連実験
・回転円盤上で、半径方向に往復直線運動する物体の軌跡を描きました。
・熱力学的効果は組み込んでいない。しかし、空気の流れが、ヒマラヤやロッキーの
山脈により変形され、蛇行が励起されたものとして考えてもよさそうです。
・位相の「ずれ」は、大気波動が西進する話について、現実味を帯びさせてくれます。
#B97 【追加実験、考察等】
・この実験は、フーコーの実験の延長線上にあります。
・ペットボトルに水を入れ、さかさまにすると、水がこぼれます。
①このとき、自分が地面に立ってじっとしたままでいると、水は1点に落下します。
②自分が一回転すると、地面には円が描かれます。
③自分がじっとしたままで、ボトルを単振動させると、地面には直線が描かれます。
④単振動させながら、自分が一回転すると、地面には波動が描かれます。
・四角い食パンを回しつつ、上から蜂蜜をたらしてみましょう。
上記①~④において、自分が食パン、水が蜂蜜になったとみなせば、同じ原理の実験になります。
(この実験に引き続き、食パン=>カロリーやエネルギー、蜂蜜=>流体の粘性、の話や実験に移行します。)
・回転円盤上で鎖を垂下させ、単振動させつつ下げていくと、波動が描かれます。(紐やネックレスでもOKです。)
この実験は、新聞紙を広げ、数人が新聞紙回転担当、一人が鎖の垂下・単振動担当、一人が、全体号令担当に
なって、協働して行うと、リチャードソンの数値予報計算の人海戦術の様子を再現するようなもの、となります。
位相がずれていく様子、及びずれに寄与する要因も体感できます。
・回転流体の中の対流の実験装置です:(詳細は → こちら を見てください。)
円盤と3重の水槽で、蛇行する波を作りました。波動の模様は、アルミの粉末で可視化しています。
円盤の駆動には模型用のモーターを組み立てて使っています。この実験は、Dishpan Experiment と
して有名です。同様実験は、数理解析研究所講究録800巻1992年119-128「傾斜対流実験で得られた
カオスへの遷移」等にも見受けられます。
私の実験装置で得られた蛇行の模様です。回転数、温度差、深さ、アルミ粉の散布程度等によって
波数が変わります。又、蛇行現象にならなかったり、なかなか蛇行に移行しないこともあります。

 トリトン流体力学、上巻、p.301によれば、この波は、「傾圧波」と呼ばれる、とあります。
・ロスビー波の実験について:
小倉先生の気象力学通論p.53~に、ロスビー波の説明と、模型実験に関する記述があります。
トリトン流体力学にも同様の記述があり、いずれもIbbetson and Phillips, 1967 を引用しています。
上述の「回転流体の中の対流の実験」において、温度差をあたえずに、中央の水槽において水槽の底面
に傾斜をつけるとβ効果を与えることとなり、円周方向に振動を与えるとRossby波が出来るようです。
【Rossby波の実験は、対流現象の存在は前提としていない、すなわちDishpan Experiment とは本質的
に異なっていると考えられます。】
【但し、Dishpan Experiment においてβ効果をあたえた場合、その時に出来るであろう波動は、
なんと呼べばよいのだろうか。「Rossby波」なのだろうか、やはり別物だろうか。】
先頭へ戻る 気象科学実験教室、一覧表 キッズの気象実験、一覧表
トリトン流体力学、上巻、p.301によれば、この波は、「傾圧波」と呼ばれる、とあります。
・ロスビー波の実験について:
小倉先生の気象力学通論p.53~に、ロスビー波の説明と、模型実験に関する記述があります。
トリトン流体力学にも同様の記述があり、いずれもIbbetson and Phillips, 1967 を引用しています。
上述の「回転流体の中の対流の実験」において、温度差をあたえずに、中央の水槽において水槽の底面
に傾斜をつけるとβ効果を与えることとなり、円周方向に振動を与えるとRossby波が出来るようです。
【Rossby波の実験は、対流現象の存在は前提としていない、すなわちDishpan Experiment とは本質的
に異なっていると考えられます。】
【但し、Dishpan Experiment においてβ効果をあたえた場合、その時に出来るであろう波動は、
なんと呼べばよいのだろうか。「Rossby波」なのだろうか、やはり別物だろうか。】
先頭へ戻る 気象科学実験教室、一覧表 キッズの気象実験、一覧表