Return Home 気象科学実験教室、一覧表　キッズの気象実験、一覧表　「気象実験クラブ」入会案内。
気象実験(#70)
実験の様子を写真で紹介します。

Originated 2008-08/08   Last Updated 2008-08/30,09/30,10/24,11/25,12/08, 2009-01/31

XPM70  剛体回転１ （回転円盤、円形の容器、ビー玉）および（コンピューターシミュレーション）
EXPM71  台風の渦巻きを描く （コンピューターシミュレーション）
EXPM72  風に流される台風 （コンピューターシミュレーション）
EXPM73  台風の中心位置の軌跡を描く （コンピューターシミュレーション）
EXPM74  フーコーの振り子 （コンピューターシミュレーション）および（回転円盤、フック、糸、紙、砂）
EXPM75  コリオリの力　（コンピューターシミュレーション）および（回転円盤、紙、定規、鉛筆）
EXPM76  方位磁石（方位磁石、回転円盤）磁針が一定方向をさす性質を利用する
EXPM77  ジャイロ（地球ゴマ、その他）　ジャイロを使って地球の回転を考えよう、
EXPM78  カオス（ローレンツのストレンジアトラクター）（コンピューターシミュレーション）
EXPM79  フラクタル（マンデルブローの図形）（コンピューターシミュレーション）



#700  実験７０
　　　・回転円盤上での直線運動は、コリオリ力により、右に曲がります。
　　　　下図のような凹凸のある場合でも右回りになります。

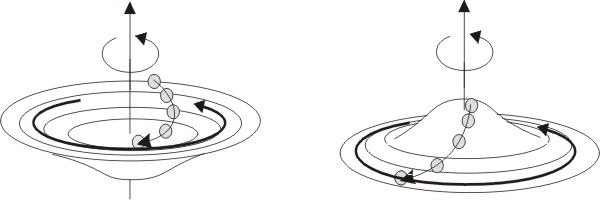　　　　コリオリ力は、空気を「進行方向の右側に曲げる」作用をします。
　　　・しかし、台風の渦は、左巻きです。
　　　・この違いをどのように説明しますか。
　　　・実験的に台風の様な左巻きの渦をつくることができるでしょうか。
        
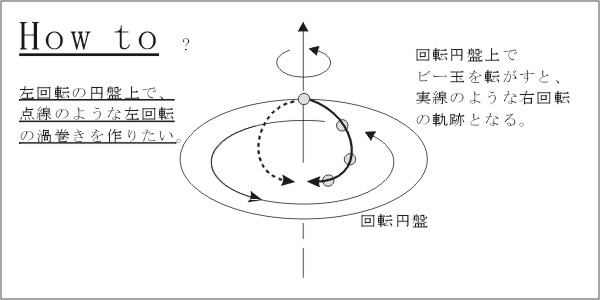　　　・「剛体回転」がキーワード、となります。
　　　・実験的に左回りの回転を実現した後、コンピューターシミュレーションを行います。
　　　
#701  実験タイトル＝剛体回転１（コンピューターシミュレーション）

#702  実験の狙い＝剛体回転と言うものを実験とコンピューターシミュレーションで体感する

水＝空気、ビー玉＝空気塊、とみなして実験



#703  実験装置の製作 and/or 準備
      ・回転円盤、直径約５０ＣＭのボール状の容器（実際には、不要になった照明器具の傘）、
　　　　ビー玉

#704  実験の実行と結果
　　　・回転円盤上に直径約５０ＣＭのボール状の容器（実際には、不要になった照明器具の傘）
　　　　を乗せ、この容器に水を８分目まで入れ、ビー玉を容器の縁で手にホールドしたまま、
　　　　全体を回転させます。
　　　・回転が強いと、水が円周から飛び散りますので、数回、手で加減しつつ回した後、
　　　　ビー玉を放ちます。このとき、水面は、回転放物面を形成します。ビー玉は上の写真の
　　　　ように容器の回転があるにも関わらず、容器の壁面にへばりついたまま回転します。
　　　・ビー玉が左回りで中心に向かっていく様子は、この実験においては、終盤に見られます。
　　　・渦巻が左回転となる様子を概念図で示します。
　
        接平面は左方向へ回転する。この接平面（地上）にある空気は、同じく左方向へ
　　　　剛体回転している。空気は気圧傾度により中心へ向かう。空気の速度は、中心に
　　　　向かうにつれ次第に大きくなる。空気は、太線の軌跡を描く。
        ★★注意！
　　　　この図に描かれている太線の軌跡の視座は、静止空間にあります。
　　　　即ち、静止空間から回転する円盤を見て、その円盤内で剛体回転しながら、円周上から
　　　　中心に向かって直線運動する物体の軌跡を見ることになります。
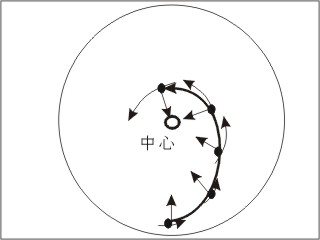　　　　★★このため、回転円盤と同じ視座にある位置から円盤と物体の動きを見たときには、
　　　　観測者には、直線運動しか見えません。
　　　　
　　　　★回転円盤と同じ視座にある位置から物体の動きを見たときに、観測者にとって、左回りになるように
　　　　見えるようにするためには、いかに考え、いかに実験すればよいでしょうか。
　　　　更なる実験と考察は、実験８０、剛体回転２において行います。
　　　
      ・水を使ったこの実験で剛体回転の感覚をつかんだら、PCスクリーン上の入力欄に数値をキーインします。
　　　・空気が剛体回転するときの角速度ω１＝地球の回転角速度ω　に等しくなることが条件です。

空気塊を剛体回転させたときの運動の軌跡 


#705  実験を効果的に行うための工夫、注意点等
　　　・特段の注意を払わなくても、容易に曲線を描くことができます。

#706  実験の解説 and/or 関連実験
　　　・水を使ったこの実験で観察される、物体の左巻きの渦は、「剛体回転＋直線運動」の結果によるものです。
　　　　このときの、視座は回転円盤上でなく円盤外の静止空間にあります。
      ・私たちは、静止空間から台風の渦を見ているのではありません。円盤上で見ています。
　　　　この実験の限界は、回転円盤上の円周方向の運動を実現できていないことにあります。
　　　　コリオリ力は、「直線運動と回転運動」の問題です。

#707 【追加実験、考察等】
　　　・台風の渦巻は、「直線運動と回転運動」に、剛体回転を加え、さらに角運動量保存
　　　　の法則も加えて説明します。

      ・地球の回転角速度と空気の回転角速度に差が生じると「風」ができます。
　　　　この議論は実験８０、剛体回転２を見てください。

先頭へ戻る  気象科学実験教室、一覧表　キッズの気象実験、一覧表


#710  実験７１
    　コンピューターシミュレーションで台風の渦巻きを描いてみましょう。
　　　子供たちに対しては、コンピューターのプログラムで、台風の渦の形を描くことが
　　　できることを話します。　

#711  実験タイトル＝台風の渦巻きを描く
　　　 
#712  実験の狙い＝コンピューターシミュレーションを体感する
　　　　　　　　　aztyphoon1010.htmへリンクする。

台風の渦巻きを「線画」で描く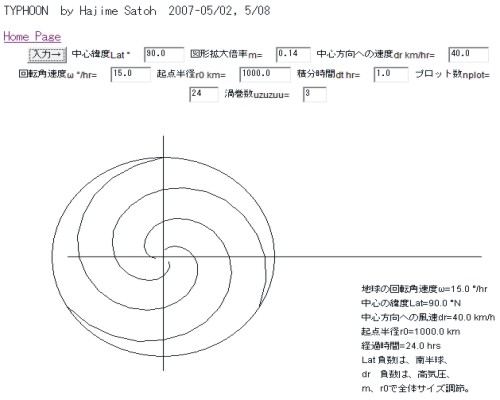


渦巻を点、包絡線、文字で描く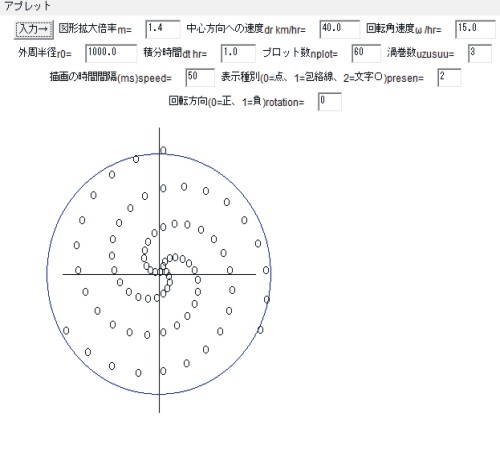

　


#713  実験装置の製作 and/or 準備
      ・PCスクリーン上で操作します。

#714  実験の実行と結果
      ・スクリーン上の入力欄に数値をキーインします。
　　　・すなわち、パラメーター（緯度、地球の自転角速度、台風の進行速度、渦数など）の値を
　　　　任意にかえてみます。
　　　・値に対応した図形が描きだされます。

#715  実験を効果的に行うための工夫、注意点等
      ・台風に関する予備知識を持っていると、的確なシミュレーションができるでしょう。

#716  実験の解説 and/or 関連実験
      ・実際の台風の渦巻は複雑です。　
　　　・しかし、空気にかかる力を単純化して考えるとき、空気の基本的な動きが現れます。
　　　・空気の動きを数式表現して、時間経過に伴う空気塊の運動の軌跡を描きます。
　　　・実際にはあり得ない値（速度、角速度など）を与えても、図形を描くことができます。
　　　　どんな形になるか。こういうことが容易にできるのは、コンピューターシミュレーションの
　　　　得意な技の一つです。　

#717 【追加実験、考察等】
　　　・高気圧性回転を加味したシミュレーションはこちらです。　（aztyphoon1010.htmへリンクする）
　　　・実験７０、剛体回転１

　　　渦巻形成の理論のベースには、渦巻を乗せる地面、土台がどの様になっているのかを知る必要があります。
　　　その地面は、「接平面」とよばれます。接平面に関しては、２つの実験を用意しました。
　　　実験８４、接平面 実験８５、接平面２

先頭へ戻る  気象科学実験教室、一覧表　キッズの気象実験、一覧表


#720  実験７２
    　コンピューターシミュレーションで台風が偏西風などの風に流される時の渦を描いてみましょう。
　　　子供たちに対しては、コンピューターのプログラムで、台風の渦の形が風によって変わることの不思議さを見てもらいます。
　　　このコンピューターシミュレーションで描かれる図形は、気象衛星雲画像で見るのとは、だいぶ違って見えます。
　　　このため、視点を変えると、見え方（すなわち、現象の形）が変わってくる話をします。
      また、気流の収束・発散の様子も見てみましょう。

　　　なお、現象の見方、観測の仕方に関しては、オイラーの方法とラグランジュの方法があります。
　　　気象観測は、オイラーの方法で行われています。この実験で描く渦の軌跡は、ラグランジュの見方である、と考えられます。

#721  実験タイトル＝風に流される台風の渦の軌跡を描く
　　　 
#722  実験の狙い＝コンピューターシミュレーションで台風が風に流されたり、或いは収束発散する様子を体感する

風に流される台風の渦の軌跡を描く 



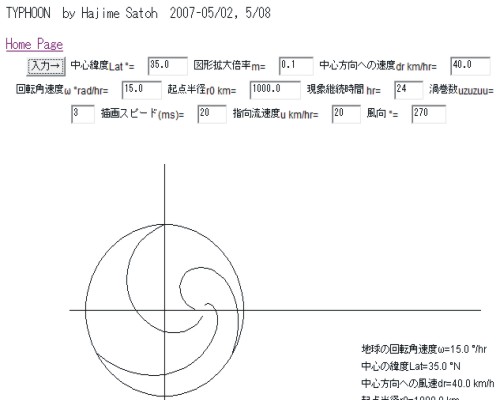
気流が収束・発散する様子を見ることができます。 




#723  実験装置の製作 and/or 準備
      ・PCスクリーン上で操作します。

#724  実験の実行と結果
      ・スクリーン上の入力欄に数値をキーインします。
　　　・すなわち、パラメーター（台風を流す風の方向や速度など）の値を任意にかえてみます。
　　　・値に対応した図形が描きだされます。

#725  実験を効果的に行うための工夫、注意点等
      ・台風に関する予備知識を持っていると、的確なシミュレーションができるでしょう。

#726  実験の解説 and/or 関連実験
      ・実際の台風の渦巻は複雑です。　
　　　・しかし、空気にかかる力を単純化して考えるとき、空気の基本的な動きが現れます。
　　　・空気の動きを数式表現して、時間経過に伴う空気塊の運動の軌跡を描きます。

#737 【追加実験、考察等】
      ・空気が運動する軌跡は、たとえば、流線として表現されます。
　　　　この流線に関しては、 実験B2、流線を観察する　を参照して下さい。

先頭へ戻る  気象科学実験教室、一覧表　キッズの気象実験、一覧表



#730  実験７３
　　　台風の中心の軌跡は、トロコイド曲線になると書いてある文献があります。
　　　トロコイド曲線を描いてみましょう。
　　　このトロコイド曲線は、同じ数式を使って、パラメーターの値の与え方によって、
　　　サイクロイド曲線にもなります。

#731  実験タイトル＝台風の中心の軌跡

#732  実験の狙い＝コンピューターシミュレーションを体感する

サイクロイド曲線、トロコイド曲線を描く 




#733  実験装置の製作 and/or 準備
      ・PCスクリーン上で操作します。

#734  実験の実行と結果
      ・スクリーン上の入力欄に数値をキーインします。
　　　・値に対応して、サイクロイド　または、トロコイドとなります。
　　　・トロコイド曲線には、ループを描く場合と、ループしない場合があります。

#735  実験を効果的に行うための工夫、注意点等
　　　・特段の注意を払わなくても、容易に曲線を描くことができます。

#736  実験の解説 and/or 関連実験
      ・台風の中心がなにゆえトロコイド曲線を描くのか、
　　　　筆者には残念ながら説明できません。
　　　　
#737 【追加実験、考察等】
      ・サイクロイド曲線は、「最速曲線」とも言われます。斜面に沿って降りるよりも、
　　　　サイクロイド曲線にそって降りるほうが早く下に着きます。


先頭へ戻る  気象科学実験教室、一覧表　キッズの気象実験、一覧表


#740  実験７４
      「フーコーの振り子」の実験は、振り子の振動面が、回転している地面に対して投影する軌跡を求める（描くこと）ことにより、
　　　地球が回転していること、を考えることを目的とします。
　　　ただし、地面と言っても「接平面」です。接平面に描かれる振り子の軌道の方程式は、力学の問題として求められます。

　　　実験としては、２種類あります。
　　　ひとつは、回転座標系と慣性座標系における振り子の運動方程式を求め、数式を数値計算し、解をパソコンのスクリーンに
　　　描くことです。数式の中には、遠心力、コリオリ力、接平面の回転が入り込んできます。
　　　パソコンシミュレーションは、「物」に起因する実験上の障害・誤差を未然に防ぐことができる利点があります。

　　　
　　　もう一つの方式は、おもりをハリガネで天井から吊り下げて、揺らすことです。（振動させます。）
　　　しかし、この実験を本当に成功させるには、実施してよく分かりますが、素人にはとても困難なところがあることに気づきます。
　　　マサツと言う実験の本質と関係のない問題が入り込んでくるのです。もっと雑駁でかつ、原理的には同じものですが、砂を使った
　　　実験を行います。

　　　この実験で地球が回転（自転）していることが納得できれば幸いです。
　　　この実験が終わったら、ぜひともジャイロの実験をトライしてみてください。

#741  実験タイトル＝フーコーの振り子

#742  実験の狙い＝フーコーの振り子による軌跡を描き、パラメーターを変化し軌跡の形を変えてみることを通し、
　　　　　　　　　変化に対する要因を認識し、背景にある自然の原理に思い至る。

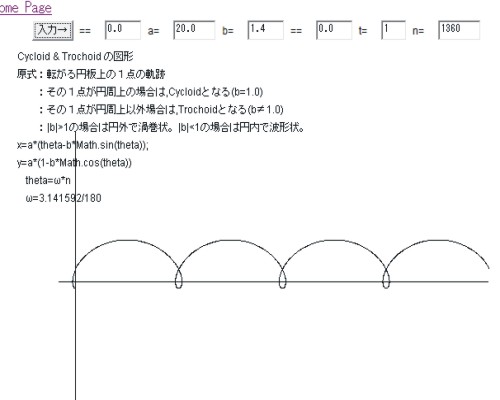
フーコーの振り子による曲線を描く



#743  実験装置の製作 and/or 準備
      ・PCスクリーン上で操作します。
　　　　操作上のパラメーターは、接平面の回転角速度a、振り子の振幅b、振り子の長さL等です。
　　　　プログラムに組み込んである数式（フーコーの振子の運動方程式）：
　　　　　　x= L*sin(ω1*t)*cos(ω0*t)
　　　　　　y=-L*sin(ω1*t)*sin(ω0*t)
　　　　　　　　ただし、　
　　　　　　　　　　ω0=(2.0*3.14/86400.0)*sin(a*rad)
　　　　　　　　　　ω1=2.0*b*rad/T
　　　　　　　　　　rad=3.14/180.0
　　　　　　　　　　T=2.0*3.14*sqrt(L/9.8)

　　　・さらに、＃７４７で、砂を使って実験します。

#744  実験の実行と結果
　　　・博物館で見るのとはずいぶん粗いですが、フーコーの振り子が描く軌跡がもとまります。

#745  実験を効果的に行うための工夫、注意点等
　　　・地球の回転は遅いので、プログラム内部で回転の角速度を速めています。
　　　・振幅や長さの与え方を、試行錯誤で変えて操作して下さい。

#746  実験の解説 and/or 関連実験
　　　・実際の地球の運動は目に見えないくらい遅いです。
　　　・この実験では回転速度をupしましたが、自然現象としては、上記の数式で運動が表現されます。
　　　　原理的には同じです。

　　　　
#747 【追加実験、考察等】
　　　・フーコーの振り子で花びらを描きます。→花びら（バラ曲線）を描く


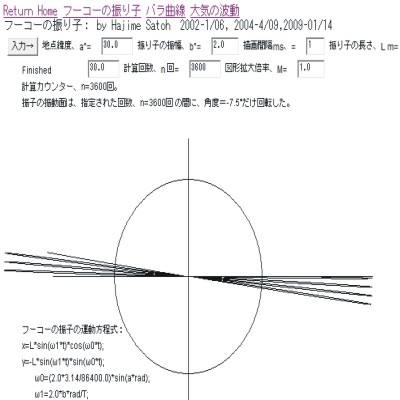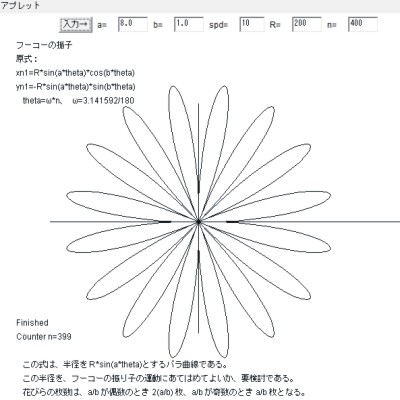      ・フーコーの振り子による軌跡を「砂」で描くことができます。
　　　・フック、針金（or 糸　or 紐）、新聞紙、砂、ペットボトル、鉄板、円盤を用意します。
　　　・細かい砂をペットボトルに入れ、ボトルの蓋の部分を砂の出口とした。
　　　　出口の口径は、竜巻の実験のときの蓋を利用
　　　　したので、８〜１０ｍｍであった。
　　　・円盤の上に鉄板を乗せ、円盤を回転し、砂を入れたペットボトルを鉛直面内に振動
　　　　させると模様が描かれる。今回の実験では、対称形の（きれいな）模様にはなっていない。
　　　・振り子が１往復する時間（２秒程度）の間に、円盤（鉄板）をおよそ２０°程度回転
　　　　すると、ある程度「マシ」なもようが得られます。
　　　・振幅が減衰したり、円盤の回転が不規則になると、図形は崩れます。
　　　　（下の写真では、ほとんどの模様が崩れています。きれいな模様を得ることは、
　　　　　結構難しいです。）
　　　・砂粒の粒径、模様の継続時間、模様の太さなど、試行錯誤して最適な状態を見つけよう。


砂で模様を描く。全景図。

砂で模様を描く。拡大図。



ある程度の「実験感覚」をからだで感じ取って、翌日実験を継続しました。

砂の粒を揃える。

砂で模様を描く。

砂で模様を描く。

砂で模様を描く。


砂で模様を描く。

砂で模様を描く。

砂で模様を描く。

砂で模様を描く。



さらに数日後、慣性座標系と回転座標系を意識して実験を行いました。

装置の全景。

直線運動物体が回転物体の上を通過時の軌跡。

直線運動物体が慣性座標系に描いた軌跡。


      実験８５、接平面２、の#854で説明していますが、接平面を水平面に展開した図形が
      フーコーの振り子の軌跡に適用可能であることを確認しておいてください。
      

先頭へ戻る  実験一覧表



#750  実験７５
      気象予報士なら知らないものはないくらいお世話になるコリオリの力を
　　　シミュレーション実験で見てみます。
　　　「進行方向の右側に曲がっていく」と呪文のごとくそらんじていますが、
　　　さて、本当に右に曲がっていくでしょうか。コリオリ力を納得的理解に至る
　　　にはどのような実験を行えばよいでしょうか。
　　　コンピューターシミュレーションとしては実験７４のフーコーの振り子と
　　　同じです。コリオリ力は、実験７１の台風の渦巻きの実験にも関係したものです。
　　　コリオリ力の説明は、子供達にとっては難しい問題ですが、台風の渦巻きの成因などの
　　　解説において、やさしくできるように考えねばなりません。
　　　
#751  実験タイトル＝コリオリの力（コンピューターシミュレーション）

#752  実験の狙い＝コンピューターシミュレーションを体感する

　　　直線運動する物体を回転座標系上の観測者が見た時のその物体の運動がどのように見えるか、
　　　をパソコン上で見てみましょう。

コリオリ力 




#753  実験装置の製作 and/or 準備
      ・実験７４と同じシミュレーションで、PCスクリーン上で操作します。

#754  実験の実行と結果
      ・スクリーン上の入力欄、特に地点の緯度や物体の速度に対応して、曲がり方がどのように
　　　　なるかに注目しましょう。
　　　・直線運動する物体が回転運動する物体上でどのようににえるか、軌跡を描きます。

#755  実験を効果的に行うための工夫、注意点等
　　　・厳密には、パソコンのモデル内の時間の流れと実空間の時間流れの動機がとれません。
　　　　地球自転の角速度や物体の運動速度は、現実の現象の通りに与えることは事実上不可能です。
　　　・しかし、角速度、速度、現象の継続時間など適宜変えて、現象の変化の様子を見ることができます。　

#756  実験の解説 and/or 関連実験
　　　・直線運動する物体を回転座標系上の観測者が見た時のその物体の運動の軌跡です。
　　　・この直線運動が回転運動として描かれるのは、その直線運動をしている物体に
　　　　実際の力が作用したものではありません。見えない力が作用したものと考え、
　　　　この力が「見かけの力」、さらには、「コリオリの力」と呼ばれているものです。

#757 【追加実験、考察等】
      ・回転円盤、紙、定規、鉛筆orペンを使って簡単な実験ができます。
　　　・紙を回転運動させておき、ペンを直線運動させます。そうすると、花びらの模様が
　　　　描きだされます。
　　　・ペンを固定したままにしておくと、１つの円が出来上がります。
　　　・この方法は、実験７４のフーコーの振り子の実験で砂模様を
　　　　描いたのと原理的に同じです。
　　　・コンピューターに描かせた時のように均整のとれた模様はなかなかできません。
　　　・円盤を回す操作やペンを直線運動する操作は、コンピューターの中では数式で
　　　　表現されています。シミュレーション画面を操作する人は、論理を知らなくても
　　　　図形を描くことが出来、頭の中で、なんとなく理解できるでしょう。
　　　　しかし、円盤を回したりペンを直線運動させたりして何度も繰り返し行うことに
　　　　よって、直線運動と回転運動の相互連携プレーを体感できるのではないかと思います。

　　　・海陸風において、例えば、海陸のあいだで風が直線運動する時の速度＝10km/hr、継続時間を4時間とするとき、
　　　　運動距離＝40kmとなります。非常に大きな振り子の運動と考えられます。
　　　　この４時間の間に北緯N°の地面は、(15*sinN)°回転するので、風向も対応してN=30のときには、30°程度
　　　　変化すると考えられます。
　　　　障害物の少ない海岸付近で、どなたか観察された記録があると、大いに参考になると思われます。　
　　　　（例えば、駿河湾奥には海岸近くに製紙工場の煙突が立ち並んでいますが、煙の方向変化を観察してみる
　　　　　ことが考えられます。）　


装置の全景

試行錯誤
 

 

先頭へ戻る  気象科学実験教室、一覧表　キッズの気象実験、一覧表




#760  実験７６
　　　フーコーの振り子の実験で振り子は、地球の回転があっても鉛直面内を運動する。
　　　この鉛直面は、方向が不変である。この性質は、方位磁石の磁針が一定方向をさす
　　　様子に似ている。方向を一定とさせる原理は異なるが、一見したところよく似ている。
　　　この類似性はごく単純なことではあるが、これまで気がつくことがなかった。
　　　フーコーの振り子の実験や、コリオリ力の実験において、関連実験として行ってみる
　　　ことをお勧めしたい。

#761  実験タイトル＝方位磁石

#762  実験の狙い＝狭い範囲の「地面」が回転しても方角は不変であることを見る。

方位磁石
  
      
円盤を３６０°回転する。磁針の方向は一定です。 





#763  実験装置の製作 and/or 準備
      ・方位磁石を円盤上に乗せ、円盤を回転する。

#764  実験の実行と結果
      ・方位磁石を乗せた円盤が回転するとき、方位磁石の方向は常に一定方向をさしています。
　　　・遊園地で、メリーゴーラウンドに乗っていても、「北」の方向は常に一定である
　　　　ことに似ています。

#765  実験を効果的に行うための工夫、注意点等
      ・方位磁石を２つ円盤上に置くと２つの磁針が平行し、かつ同じ方向を向くことがわかる。

#766  実験の解説 and/or 関連実験
      ・磁針は磁力の力によって常に磁力線の方向に向きます。
　　　・実験規模がごく小さいので、磁針が一定方向をさすことを擬似的に
　　　　【羅針盤のコマの回転方向が一定であることとして】見ることができる。
　　　・また、この実験の回転は、剛体回転とも異なることに注意してください。

#767 【追加実験、考察等】
　　　・磁力線によって磁針が一定方向を向くことを、慣性の法則に従う運動に関連付ける
　　　　ことは本来無意味であるので、ここはひとつ、実験７７、ジャイロスコープの実験
　　　　を行わざるを得ない。


先頭へ戻る  気象科学実験教室、一覧表　キッズの気象実験、一覧表


#770  実験７７
　　　コマを台に乗せ、コマの回転軸を傾けたまま回転させます。台が自由に運動できるように
　　　しておくと、その台も回転を始めます。しかも、回転軸の角度に応じて台の回転速度は
　　　異なります。こういう現象に気づいたのです。

　　　さて、地球が自転していることは、太陽や星の動きで分かります。
　　　そして、フーコーの振り子の実験では、地軸に傾きをもつ平面（地面＝接平面）が回転
　　　していることが実証されています。
　　　しかし、なんとなく、「ピン」と来ない気がします。気象予報士の専売特許みたいな
　　　「渦度」にsinθを乗算する話も、しかりです。一つの回転が存在して、その回転軸Ａに
　　　傾きのある別の回転軸Ｂを考えるとき、回転軸Ｂをもつ物体も回転する、と教えられて
　　　きました。「へ〜そんなものか」、と。

      ここでの実験は、ごく小さい規模で、見やすいサイズと時間で、コマの動きと水平面の
　　　動きの関係を観察します。


      なお、接平面の回転角度は、その地点の緯度に応じて変化します。この理論的証明は拙著の
　　　シリーズ＃２「天気図と気象理論」のP.114 に掲載しています。
　　　一部写真が不鮮明なところもありますが、本文やイラストを参照してみてください。
　　　
#771  実験タイトル＝ジャイロ

#772  実験の狙い＝傾いた回転軸を有するコマ（ジャイロスコープ）の回転運動により励起される
　　　　　　　　　水平面の回転運動を観察する。
装置の全景

回転軸の傾きをさまざまに(90N、45N、0N)変えてみる


#773  実験装置の製作 and/or 準備
      ・ジャイロ、バケツ、プラスチック容器、ペットボトル、水を用意します。
　　　・ペットボトルの胴体部分を切り離し、ジャイロを乗せる架台とします。
　　　・バケツに水を入れ、プラスチック容器を浮かべます。
　　　・ジャイロを回し、架台に乗せ、架台をプラスチック容器の中央部に静かに置きます。
　　　・ジャイロを架台に乗せるとき、ジャイロの傾きを「鉛直、４５°、水平」の３種類とします。

#774  実験の実行と結果
      ・ジャイロの傾きに応じて、プラスチック容器が回転します。
　　　・１分あたりの回転数をカウントします。５回ずつ実験し、回転数のうち、最大値と最小値を
　　　　除いた残りの３つのカウントの相加平均を求めます。以下の回数となりました。


回転軸の傾き
カウント数
平均値

90（°）
11,12,11,11,12
11.3
45（°）
06,08,07,06,08
7.0
00（°）
00,00,00,00,00
0.0


#775  実験を効果的に行うための工夫、注意点等
      ・プラスチック容器が回転するとき、バケツの内壁にこすれることがあります。
　　　　できるだけマサツが小さくなるような容器材質が望ましいです。

#776  実験の解説 and/or 関連実験
　　　・回転体上の平面（接平面と言う）の回転運動を推定しようとするものです。
　　　・フーコーの実験で、観測地点の地面の回転角速度は、地球の自転の角速度にその地点の
　　　　緯度の正弦値を乗じた値になることを知りました。
　　　・この実験では	sin(45°)=0.70 ですから、11.3*0.70=7.8  の値が得られるべきでしょう。
　　　・しかし、マサツなどの影響のためか、実測値は、7.0 とやや少ない目でした。

　　　・この実験で注意すべきは、コマの回転方向とプラスチック容器の回転方向です。
　　　　同じ方向であるべきですね。　　さらに言うならば、接平面上を直線運動する
　　　　物体を考えるとき、観測者が接平面上に立って物体を見ているとき、その物体は、
　　　　接平面の回転方向とは逆方向に回転しているように見えます。
　　　　フーコーの実験　や　コリオリの実験　で見てきました。
      　他にも、関連実験として、方位磁石の実験を参照して下さい。

#777 【追加実験、考察等】
　　　・下の写真のようにジャイロを手に持って、その回転軸を傾けると抵抗する力を感じ、
　　　　平行移動すると抵抗を感じません。コマのように回転している物体は、その回転軸を
　　　　一定に保とうとする性質があり、回転軸を傾けようとして外力を加えると元に戻ろう
　　　　とします。それが抵抗する力であり、コマ自身が自分の姿勢を保とうとする性質の現れです。
      ・話は飛躍しますが、「角運動量保存の法則」の実例です。
　　　　この実験においては、「コマ、架台、プラスチック容器」の３者から構成される一つの
　　　　「系」において、コマの持つ角運動量が架台を経由して、プラスチック容器に伝えられた、
　　　　と考えます。

手にもって回転軸の方向を変えようとすると抵抗を感じる。




先頭へ戻る  気象科学実験教室、一覧表　キッズの気象実験、一覧表


#780  実験７８
　　　気象学者ローレンツが対流の研究で数値計算を行っていた時に発見した
　　　カオス現象。その原点となった数式を数値計算して解を求め、図形に描いてみましょう。

#781  実験タイトル＝カオス（ローレンツのストレンジアトラクター）

#782  実験の狙い＝コンピューターシミュレーションを体感する

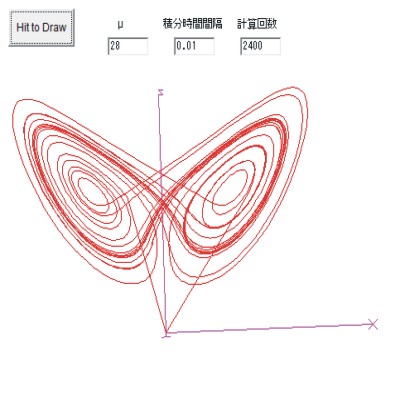
カオス（ローレンツのストレンジアトラクター）




#783  実験装置の製作 and/or 準備
      ・PCスクリーン上で操作します。

#784  実験の実行と結果
      ・スクリーン上の入力欄に数値をキーインします。
　　　・μの値に対応して、収束する図形や発散する図形などがえがかれます。
　　　・操作の説明はこちらを参照

#785  実験を効果的に行うための工夫、注意点等
      ・Ｘ、Ｙ、Ｚの３Ｄ図形です。画面をドラッグして回転してみてください。
　　　・描かれる曲線が、どんなに接近しているように見えても重なることはありません。

#786  実験の解説 and/or 関連実験
　　　・ローレンツモデル：
　　　　　　∂ｘ/∂ｔ=−γｘ＋γｙ
　　　　　　∂ｙ/∂ｔ＝−ｘｚ＋μｘ−ｙ
　　　　　　∂ｚ/∂ｔ＝ｘｙ−ｂｚ
　　　　★μは、平行平板の上下面の温度差ΔＴに比例した数字です。
　　　　　この温度差が拡大して行くと、流体は安定状態から対流へと
　　　　　次第に不安定かつ複雑な動きへと変わっていきます。
　　　　　熱の移動の仕方は、「熱伝導→対流→沸騰」、と変わっていきます。
      ・描かれる曲線と実際の対流現象との対応はなかなか困難ですが。
　　　　専門書には解説があります。

#787 【追加実験、考察等】
      ・拙著「天気図と気象理論」の理論の基礎、数値予報（４）P.127に
　　　　数値予報のための若干の関連記事を掲載しています。ご参照ください。


　　　・カオス図形を描く→カオス、フラクタル、自然現象

先頭へ戻る  気象科学実験教室、一覧表　キッズの気象実験、一覧表



#790  実験７９
      フラクタル幾何学の創始者、マンデルブロー博士はその名前を冠した「マンデルブロの図形」
      で有名です。どんな図形か描いてみます。
      そして、自然界の中における相似的な形をした物体や現象にはどんなものがあるか探して
　　　見ましょう。

#791  実験タイトル＝フラクタル（マンデルブローの図形）

#792  実験の狙い＝コンピューターシミュレーションを体感する

      マンデルブローの図形を描きます。



#793  実験装置の製作 and/or 準備
      ・PCスクリーン上で操作します。

#794  実験の実行と結果
      ・スクリーン上の入力欄に数値をキーインします。
　　　・描いた図形の任意の場所をクリックすると、物と同じ形の相似的な図形が現れてきます。
　　　・どんどんクリックして行っても同じ図形が現れてきます。
　　　　（ただし、計算精度により限界があります。）

#795  実験を効果的に行うための工夫、注意点等
      ・相似的な図形の出現に注意してください。
　　　・クリックする場所は、有意な画像の「縁」の付近をえらぶと、相似的な図形が
　　　　継続して現れます。

#796  実験の解説 and/or 関連実験
      ・自然界の中にはさまざまな相似的な地形や現象があります。
　　　・たとえば、樹木の枝構造、雲の形、海岸線の形など、、。

#797 【追加実験、考察等】
　　　・ＰＣに図形を描かせるとき、計算回数が数万回の場合は、計算所要時間が数分かかる場合
　　　　があります。画面をクリックした時、反応がなくてもしばらく待ってください。
　　　・関連リンクです：
　　　　　　未来館でのマンデルブロー博士の講演　
　　　　　　EXCELで作ったフラクタル画像
　　　・以下、マンデルブローの図形を含め、その他のフラクタル図形を描きます。


#
関数
 Domain
Ｒ，Ｉ
判定条件
初期値
(x0,y0)
複素定数
(A,B)
Cacl.
画像



01
f=z2+C
 Mandel2dim 
-2.0〜0.5,
±1.2
 x2+y2>4
 (0,0)
 A=f1(R,I)
B=f2(R,I)
 50 






02
f=z3+C
 Mandel3dim 
±2,±2
 x2+y2>4
 (0,0)
 A=f1(R,I)
B=f2(R,I)
 50 






03
f=z4+C
 Mandel4dim 
±2,±2
 x2+y2>4
 (0,0)
 A=f1(R,I)
B=f2(R,I)
 50 







04
f=z2+C
Julia2dim
±1.5,±1.5
 x2+y2>4
x0=f1(R,I)
y0=f2(R,I)
 A=-0.3,
B=-0.63
 200 
  





05
f=z3+C
Julia3dim
±1.5,±1.5
 x2+y2>4
 x0=f1(R,I)
y0=f2(R,I)
 A=0.2,
B=1.1
 100 
  





06
f=z4+C
Julia4dim
±2,±2
 x2+y2>4
 x0=f1(R,I)
y0=f2(R,I)
 A=-0.3,
B=-0.63
 100 
  





07
f=z(z+C)/(1+C~z)
Blaschke00
±5,±5
 x2+y2>10
他１点
 x0=f1(R,I)
y0=f2(R,I)
 A=0.82,
B=0.00005
 100 






08
f=z(Z+C/(1+C~z)
Blaschke01
少々時間を要す
±10,±10
 x2+y2>10
他１点
 x0=0.00001,
y0=-0.0005
 A=f1(R,I)
B=f2(R,I)
 50 






09
f=z3-3pz+C
Milnor00
p=-0.5
±1.5,±1.5
 x2+y2>9
他２点
 x0=f1(R,I)
y0=f2(R,I)
 A=0.222,
B=0.124
 100 
 





10
f=λsin(z)
Sine 
±8,±8
 abs(xn)>10
abs(yn)>10
 x0=f1(R,I)
y0=f2(R,I)
 A=-1.0,
B=0.0
 40 
 





11
f=z2+C; Mandel
Julia集合Search用
±2.0,±2.0
 x2+y2>4
 (0,0)
 A=f1(R,I)
B=f2(R,I)
 50 





z=x+yi; C=A+Bi; Domain=(R=rs〜re,I=is〜ie) ← rやiは実部・虚部を、sやeは起点・終点を表す。
Screen=widthxheight=720x720; ｆ1(R,I)=rs+xx(re-rs)/width, f2(R,I)=is+yy(ie-is)/height; 

xx,yy はscreen上の座標(0〜720)。上表で、複素定数(A,B)に数値が入っている図形は、(A,B)を任意に

キーインし変更可能で、様々な図形が描かれます。# 欄Clickで右端の画像を表示・

先頭へ戻る  気象科学実験教室、一覧表　キッズの気象実験、一覧表

Return Home 
気象科学実験教室、一覧表　キッズの気象実験、一覧表　「気象実験クラブ」入会案内。
AZURE　WINFORT